本記事は
【Advent Calendar 2024】
2日目の記事です。
🌟🎄
1日目
▶▶ 本記事 ▶▶
3日目
🎅🎁

ネットコムの岩﨑です。もういくつか寝るとお正月ですね。皆さんはお正月には何をしますか?そうですね、コマを回して遊びますよね。コマは中心にある棒を「軸」として回転させることで楽しむ遊びです。というわけで、今回は「軸」についての話をしていきたいと思います。
この記事に書いてあること
- IT系の分野に出てくる「軸」について
この記事に書いていないこと
- IT系以外の分野の「軸」について
はじめに
みなさんの「軸」との初めての出会いはいつでしょうか。先に挙げたコマはかなり小さいころに見ていますが、筆者が初めて「軸」と認識したのは、小学校の算数や理科で出てくるようなグラフの「横じく」「たてじく」だったと思います。「横じく」「たてじく」は数学の世界では皆さんもよく親しんだ「x軸」「y軸」に相当し、点の位置を把握して平面上の情報を得ることができます。情報の世界でも、画面上の位置を示す座標系などで軸の考え方が不可欠です。本記事では、算数や数学における座標軸と情報技術における座標軸の相互理解を目的に、様々な「軸」について紹介していきます。
座標軸とは
座標軸とは、二次元三次元を問わず空間内の点を位置づけるための基準となる直線のことです。この章では様々な座標系の軸を紹介してきます。
平面座標系の軸
平面座標系とは、平面と名のつく通り二次元空間における点を位置づける枠組みで、二次元座標系とも呼ばれます。座標軸はx軸とy軸の2本の直交する直線で構成されており、交点を「原点」と呼びます。原点を基準として他の任意の点の位置を示し、通常 (x, y) の形式で座標を表します。
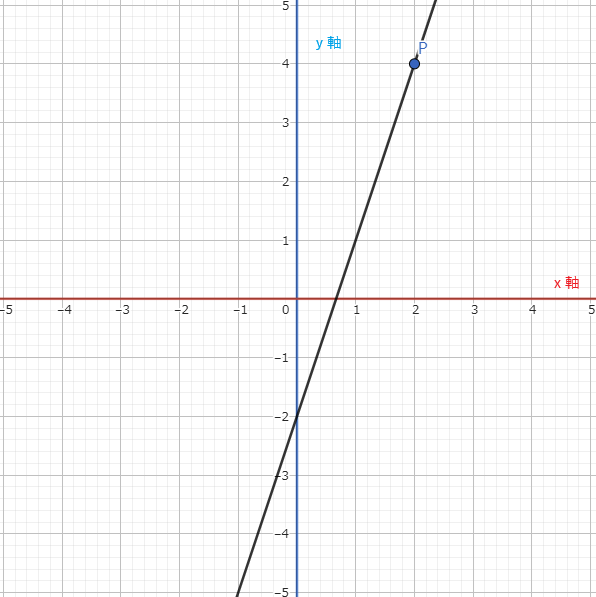
平面座標系には「デカルト座標系」「極座標系」と呼ばれる座標系があります。「デカルト座標系」はよく見る一般的な平面座標系のことで、関数のグラフなどの直線的な表現をすることが得意です。座標によって点の位置を直接的に示すことができるため、数値的にも視覚的にも点の位置が理解しやすいです。
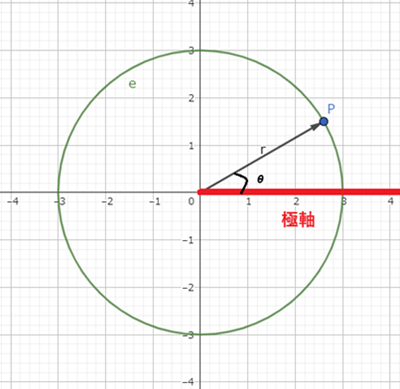
一方の「極座標系」は円などの曲線を表現することが得意です。高校数学で学んだ人もいるのではないでしょうか。極座標系では原点「O」からx軸と同じ方向に伸びている「極軸」とよばれる直線が設定されています。座標は原点からの直線距離を示す極半径 r と極軸を基準にした角度を示す極角 θ によって示し、(r, θ) の形式で表します。「デカルト座標系」の (x, y) と「極座標系」の (r, θ) は (x = r / cosθ, y = r / sinθ) の式で相互に変換することが可能です。
三次元座標系の軸
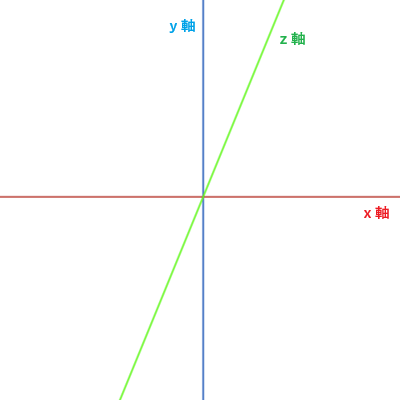
三次元座標系は平面座標系(二次元座標系)に次元が追加された座標系で、立体的な空間における点の位置を示します。x軸とy軸に加えて、それらと直交する「z軸」によって奥行きを示し、任意の点の座標は (x, y, z) の形式で表します。三次元座標系とは主に「デカルト座標系」のことを指しており、二次元のデカルト座標系に奥行きの考えが追加されたものになります。なお、極座標系は三次元の世界では「球座標系」と呼ばれ、方位角 Φ が追加されるのですが、分類としては三次元座標系ではなく「曲面座標系」に含まれるため、今回は取り上げません。
IT系における座標軸とは
情報技術においても座標軸は不可欠です。特に、データの可視化やコンピュータグラフィクス(Computer Graphics:CG)、ゲーム開発の領域において、位置や動きを表現することに使われます。この章では、先に挙げた座標系が情報技術でどのように使用されているかを紹介し、座標軸の働きについて説明していきます。
IT系における平面座標系の軸
データの可視化
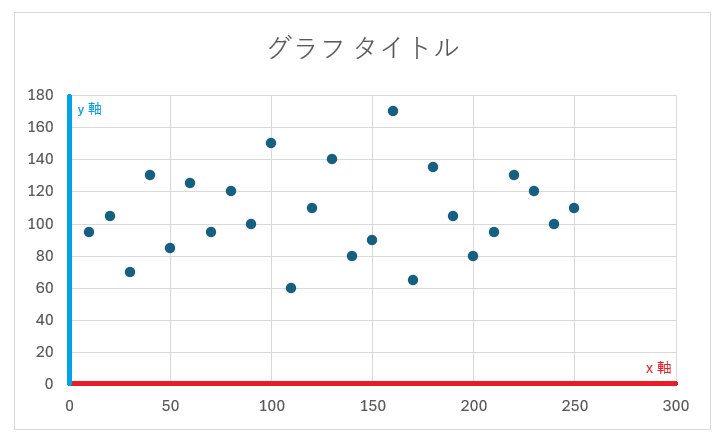
情報技術の中で平面座標系を用いる代表的な場面として、データの可視化や2DCGが上げられます。データを可視化するには表やグラフにするなどいろいろな方法があると思います。皆さんもExcelでグラフの作成をしたことがあるのではないでしょうか。その中でも「棒グラフ」や「ヒストグラム」「折れ線グラフ」「散布図」には「横軸」「縦軸」がありますね。特に「折れ線グラフ」や「散布図」にはデカルト座標系を用いることが多いです。折れ線グラフであれば月ごとの平均気温の推移を表せたり、散布図であれば身長と体重の相関を確認したりすることができます。このように、軸に適切なラベリングをしてデータを可視化することで解釈が容易になります。
2DCG
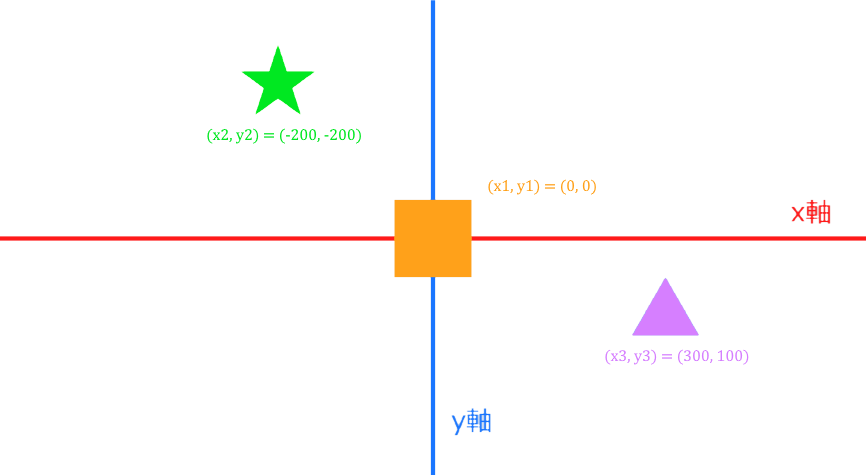
2DCGにおいても平面座標系は活用されています。例えば、映像編集ツールにも座標軸は用いられており、オブジェクトの位置を平面座標系で指定することによりシーン内への正確な配置が可能になります。また、始点と終点の座標を指定することでオブジェクトのアニメーションを簡単に表現することも可能です。
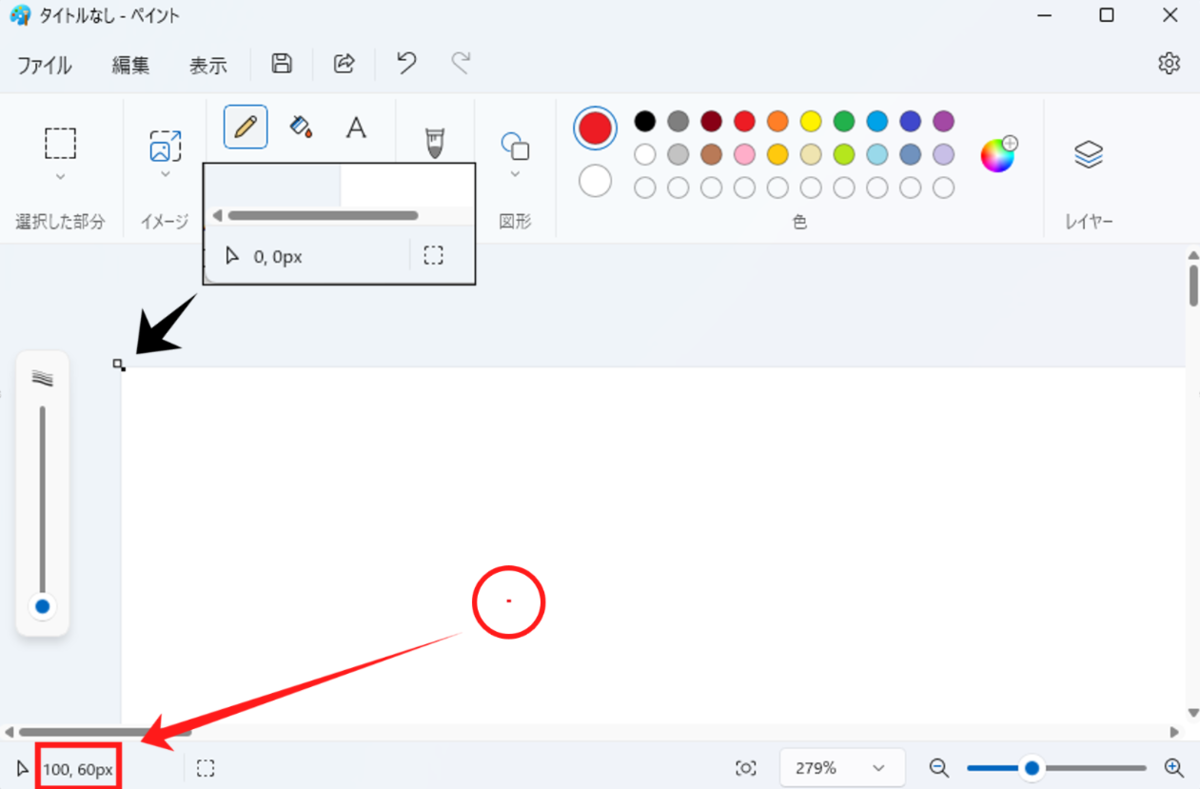
また、ディスプレイの座標を表すには「画面座標系」という座標系が用いられます。画面座標系は平面座標系とは違い、原点が左上に固定されておりy軸が下向きに伸びていることが特徴です。以下の画像はWindowsに標準搭載されているペイントソフトですが、左上の黒点が (0, 0px) と示されているのに対して、赤点は (100, 60px) と示されています。
IT系における三次元座標系の軸
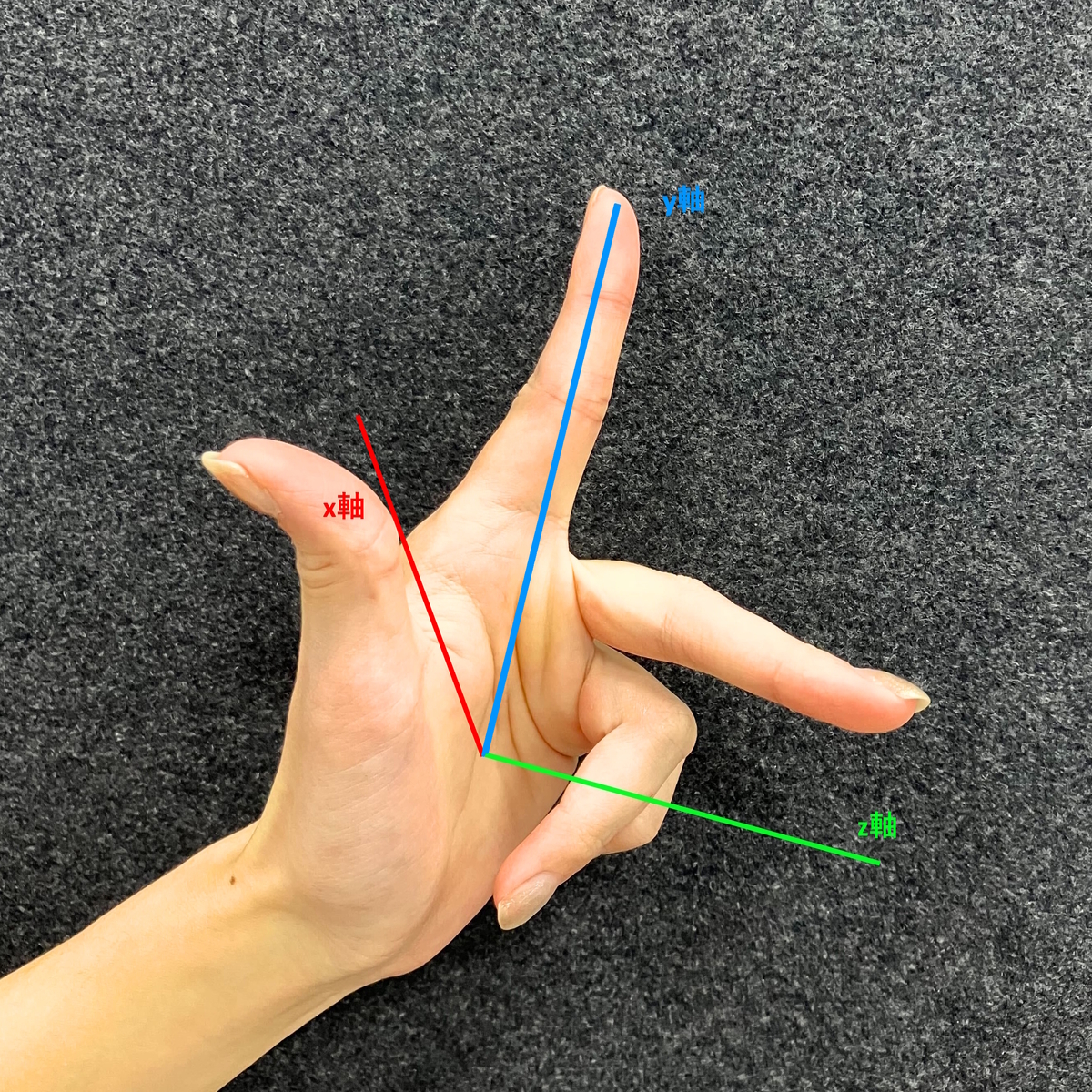
三次元座標系も情報技術の中ではよく使われており、代表的なところでは3DCGやゲーム開発などが挙げられます。三次元座標系は大きく分けて「右手系」と「左手系」の二種類があります。「右手」「左手」とは、フレミングの法則のように座標軸を手の指で表現したものになります。どちらの座標系も、親指がx軸・人差し指がy軸・中指がz軸を表しています。ここではそれぞれの座標系の代表的な使われ方を紹介していきます。

三次元座標系(右手系)
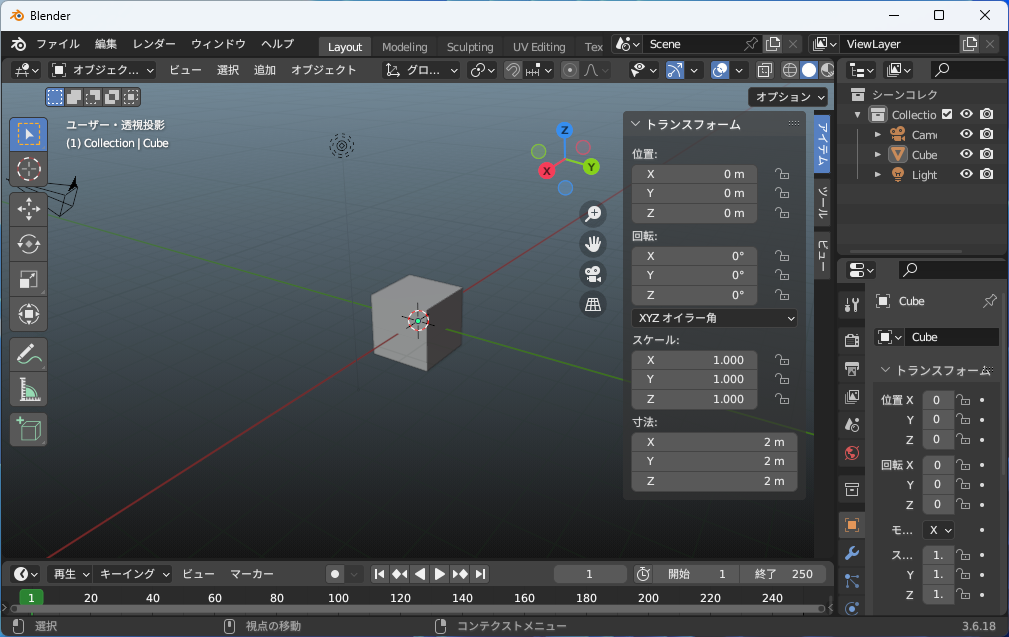
右手系は「Blender」や「Maya」「3dsMax」など、多くの3DCGのソフトウェアで用いられており、「OpenGL」のように3DCGの歴史の初期の頃から採用されています。三次元ではないですが先に挙げた平面座標系が右手系にあたるため、開発者が直感的に理解しやすかったことが採用された理由として考えられます。他にも図面作成のソフトウェアである「AutoCAD」や「Fusion360」なども右手系であることから、広く採用されていることがわかります。
三次元座標系(左手系)
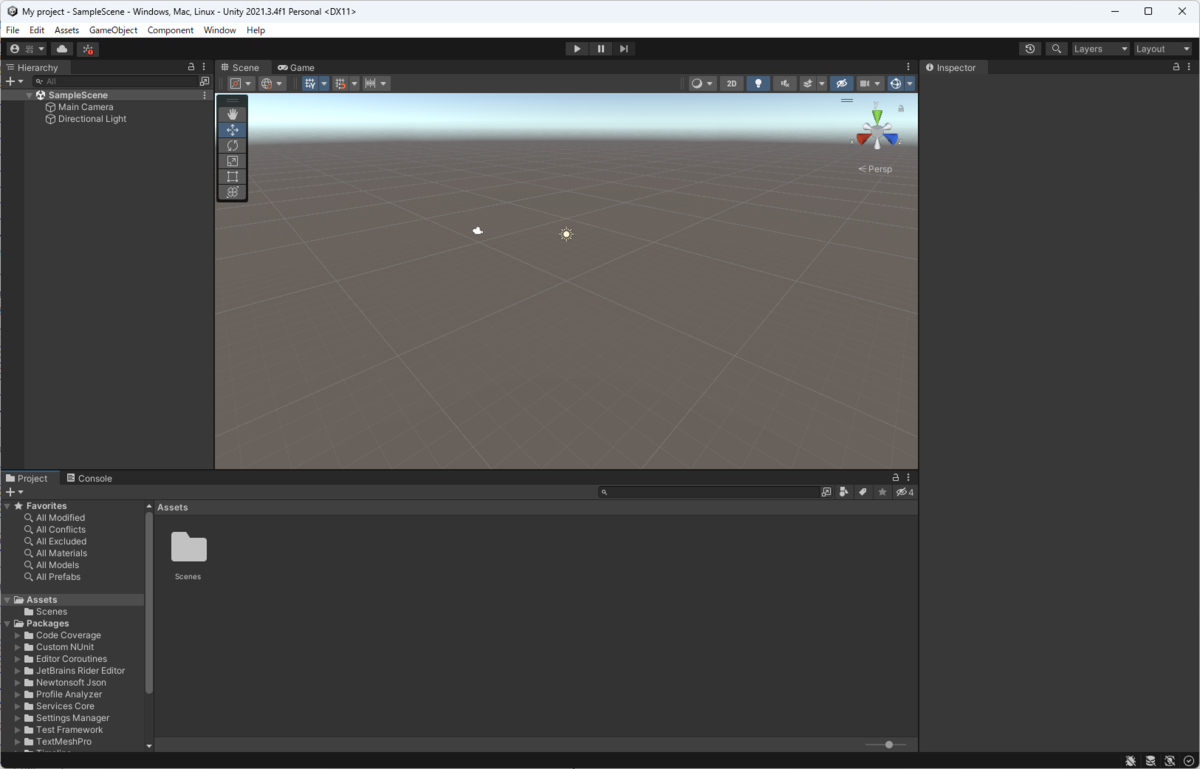
左手系は「Unity」や「UnrealEngine」などの代表的なゲームエンジンで用いられています。こちらもゲーム開発の歴史の初期に誕生した「DirectX」の影響を受けていると思われます。ゲーム開発では、右手系のモデリングツールで作成したオブジェクトを左手系であるゲームエンジンにインポートする、という作業が頻繁に行われます。そのため「モデリングツールでは正しい方向になっていたのにゲームエンジンに持ってくると向きが変わっていた」なんてことも多々あります。
また、今回は取り上げませんが、右手系や左手系といった分類の他に「Y-Up」「Z-Up」などの考え方があったり、各ソフトウェアで単位が異なっていたりするため、各ソフトウェアの特徴は意識しておきたいところです。
まとめ
ここまで座標軸の説明と情報技術の分野で用いられる座標系の紹介をしてきました。普段の生活で座標軸を意識する場面はほとんどないかと思いますが、我々の生活の中では様々な座標軸を用いて作られたものであふれているはずです。今この記事を読んでいるスマートフォンやパソコンにしても、UIには画面座標系の考えが用いられていたり、ハードの設計には右手系の三次元座標系を採用している図面作成ソフトが用いられたりしているかもしれません。皆さんもこの冬はコマを回して遊びながら「軸」について考えてみてはいかがでしょうか。
おわりです。
